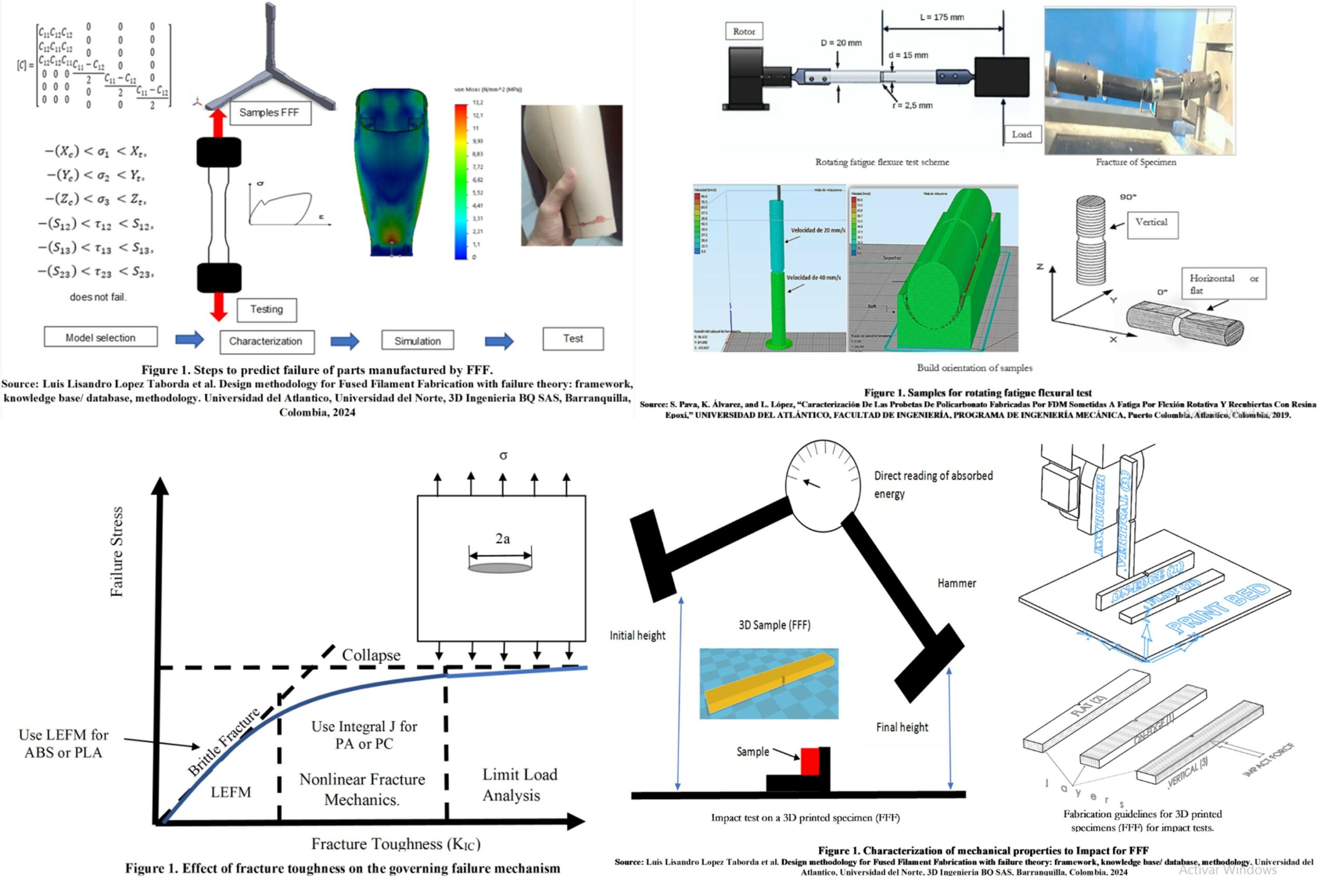
The process of failure prediction of a part starts from: 

• The definition of a specific model corresponding to an actual situation and the nature of the material.
• The model inputs determine the minimum number of tests to characterize the material and feed the model.
• Subsequently, using finite element simulation, the part is subjected to an actual load state, and the stress state is obtained from the simulation.
• The stress state feeds the predictive failure model, which determines its failure and, if not, its safety factor.

As it can be concluded from the bibliographic review, there are criteria to predict the failure of the printed parts; the uncertainty will depend on different factors, such as:

• Manufacturing materials.
• Specific technology: FFF or FDM.
• Manufacturing parameters.
• Models used.
• Type of load.
• Geometry type: 2D or 3D.
• Behavioral assumption: brittle or ductile.
• Specific mechanical characterization requirements.

The failure theory database generally provides sufficient numerical data to make the decision, implicitly including the necessary resources to adequately characterize material to use a specific failure model.

It is generally recommended that the decision to use a specific model be made based on a decision matrix due to the many aspects to be considered, at least in static failure cases. These aspects to consider in the decision matrix would be:

• The accuracy of the model
• The specific circumstances of the application
• The number of characterizations and cost required to use the model.

Other specific recommendations:

• For fracture mechanics failure cases, the method will essentially depend on the type of material, ductile or brittle, and for the fatigue case, there are few references.
• Specifically, if the stress state is simple, comparing it with the simple resistance determined from uniaxial or similar tests is recommended.
• If the stress state is 2D or 3D, using a failure model of the composite laminate theory is recommended. A maximum stress theory may be sufficient for brittle materials, and a model such as Tsai-Hill may be more accurate.
• An isotropic model averaging the anisotropic properties is sufficient for deformation prediction, although more accurate than an anisotropic one.

It is recommended to remember the following points when considering mechanical properties and characterizations from the literature.

• The mechanical properties reported by manufacturers do not correspond to those of mechanical characterizations in scientific articles and are above scientific values.
• The properties of a material can vary from supplier to supplier.
• Mechanical properties vary from industrial to desktop machines for reasons such as the high temperature of the heating chamber, which desktop printers lack.
• Mechanical properties may vary depending on the type of specimen used for testing, the size of the nozzle, or the number of perimeter layers.

Mechanical properties vary with all manufacturing parameters, such as orientation, layers, layer height, and filler percentages. However, they do not follow a fixed trend for all materials. The recommendation is to mechanically characterize the materials and parts built with the materials purchased and available from local suppliers. Consider combining other processes to improve mechanical resistance, such as coatings and galvanizing, infiltration of materials and resins, addition of elements in the filament, and thermal treatments.

It is also possible to redesign a consolidated part, in an assembly of several parts considering the following possibilities:

• Different Parts of a single material manufactured by FFF, but with different process parameters each, such as orientation, percentage of filler, among others.
• Parts of different materials all processed by FFF, with the same or different process parameters each one.
• Parts of different materials processed by FFF and other processes.